Zadání domácího úkolu
V letošní závěrečné eseji nebudete příliš limitováni – vyberte si určitou partii matematiky a napište mi o ní pojednání v minimální délce 11 palců před vložením do adminu. Pod touto partií ale rozumějte spíše konkrétní jevy, které jsou zajímavé a takříkajíc kouzelné, které dokáží zaujmout i laika – viz například problematika zlatého řezu, zrcadlová čísla, tři problémy starověké geometrie a tak dále; vyberte si sami, o čem se chcete a dokážete rozepsat, budu se na vaše práce těšit. :-)
Vypracování
Dlouho jsem nevěděla, o čem vlastně budu tuto esej psát. Pátrala jsem a sháněla informace, což se naštěstí nakonec vyplatilo a objevila jsem „oblast“ matematiky, která mě zaujala svou bohatou historií a neobvyklou hravostí, se kterou vystupuje. Dokonce i trochu pasuje do našeho světa kouzel a mohla by zaujmout i zapřisáhlé odpůrce mudlovin.
Jedná se o magické čtverce. Magické proto, že v sobě určitě nějaké to kouzlo skrývají, čtverce díky jejich tvaru. Podle přesné definice je magický čtverec čtvercová tabulka čísel, která má v každém řádku, sloupci i na diagonálách členy se stejným součtem. Většinou se v tabulce smí objevit každé číslo pouze jednou a normální magický čtverec je tvořen pouze přirozenými čísly.
HISTORIE
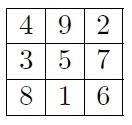
Mezi nejznámější magické čtverce patří jeden s názvem "Saturn", neboli "Lo-shu".
První zmínka o tomto čtverci padla v jednom z nejstarších dochovaných textů čínské civilizace s názvem I-ťing, který je starý více než 4 000 let. Spis I-ťing dodnes velmi ovlivňuje celou čínskou filozofii a podtrhuje tak svou přirozenou důležitost.
Mnohem větší poetičnosti se Lo-shu dostalo až okolo roku 650 př. n. l., kdy byla sepsána legenda, podle níž byl tento čtverec napsán na krunýři magické želvy objevené při záplavách císařem Yu a tak se Saturn dostal na zemský povrch.
Ale popojděme trochu v čase. Po mnohá staletí nesehrály magické čtverce žádnou zásadnější roli. Z Číny se pomalu ale jistě rozšiřovaly do světa, kde stále čekaly na někoho, kdo by se jim více věnoval. Je známo, že důmyslní Arabové sestrojili magické čtverce o straně 5 a 6 políček. Většího rozkvětu se jim dostalo až v Evropě v 15. století, kdy o nich napsal rozsáhlý spis Ital Luca Pacioli. Na něj navázal v roce 1510 Heinrich Cornelius Agrippa, který přiřadil jednotlivé čtverce planetám a jejich využití přikládal k vyvolávání andělů a ďáblů.
Za zmínku pak také stojí Paracelsus, známý lékař, alchymista a astrolog z přelomu 15. a 16. století, který využil magické čtverce k léčebným účelům. Dokonce sepsal dílo s názvem Arcidoxa Magica obsahující návody na výrobu "léčebných pečetí" zdobených těmito čtverci.
Stalo se vícekrát, že se tato část matematiky objevila i v jiných vědních disciplínách.
KONSTRUKCE
I když od prvopočátků magických čtverců ve staré Číně uběhla již dlouhá doba, stále zůstávají relativně neprozkoumaným matematickým prvkem. Dnes již dovedeme některé čtverce sestrojit, za samozřejmost pokládáme, že čím více "políček" čtverec má, tím více možností k jeho vyplnění a proměně na "magický" se nám nabízí.
Čtverec o rozměrech 3x3 políček má jen jedno správné řešení, o jednu řadu políček větší jich má už 880 a u čtverce 5x5 políček máme celých 27530522 možností. Odhadovaný počet možných čtverců o stranách 6x6 políček je dokonce 1,8 . 1017.
Byla také snaha vytvořit magický čtverec pouze z prvočísel. Dávno byl známý jeden o velikosti 4x4 políčka, ale schopní matematici toužili po objevení nějakého, který by byl z prvočísel jdoucích za sebou, což se tomuto bohužel nepodařilo.
Až v roce 1988 objevil Harry Nelson magický čtverec s devíti po sobě jdoucími prvočísly. A jistě to pro něj nic jednoduchého nebylo.
Existují také laické návody na sestrojení magického čtverce. Záleží na velikosti tabulky, kterou si chceme vytvořit - nejjednodušší jsou ty s lichým počtem postranních čtverečků. V jejich případě stačí pouze vpisovat do čtverce čísla v předepsaném pořadí.
O něco složitější je sestrojení čtverce se stranou o sudém množství čtverečků, které je navíc možné dělit 4. Zbylé případy jsou pak nejsložitější.
UMĚLECKÁ STRÁNKA
Magické čtverce v sobě kromě svého kouzla ukrývají i určitý estetický význam. Mohou mít rozmanitou symboliku, od barvitého způsobu vyjádření přesného data až po vystihnutí nálady či atmosféry.
Proto si získaly značnou oblibu i umělců, objevují se v různých malířských i architektonických dílech.
Asi nejznámější je v tomto směru německý malíř z 15. až 16. století - Albrecht Dürer, který umístil magický čtverec do své rytiny s názvem Melancholie.
Čtverce si můžeme povšimnout vpravo nahoře "na stěně". Jeho detail vypadá asi takto:
Existuje mnoho spekulací o tom, proč si autor vybral zrovna tento čtverec jako doplněk ke svému dílu. Jedno je ale téměř jisté - prostřední čtyři čísla v posledním řádku udávají letopočet 1514. V tomto roce zemřela Dürelova matka a pravděpodobně vznikla i tato rytina.
Na základě Dürela vznikaly i další čtverce podobného ražení. S drobnou úpravou je například na stěně katedrály Sagrada Familia v Barceloně.
Tento magický čtverec je poupraven tak, aby součet jeho číslic v řádcích a sloupcích udával věk, ve kterém zemřel Ježíš Kristus.
Magické čtverce jsou samy o sobě tak trochu uměleckými díly. Provázely nás napříč tisíciletími a Merlin ví, jak dlouho a jak intenzivně nás ještě provádět budou. Jejich hodnota je ale v mnoha směrech nevyčíslitelná.
_____________________
To by bylo k eseji tak nějak vše :) Děkuju moc za tak skvělý předmět a také za všechno, co jste mi za ten půlrok stihl vtlouci do hlavy.
Mějte se krásně!
Kirsten